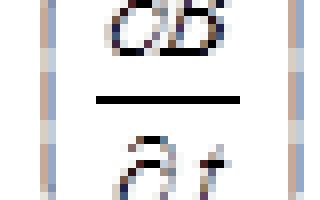Что такое ток смещения
Ток смещения
Уравнения Максвелла
Теория электромагнитного поля, которая была предложена Фарадеем, была математически и логически завершена в работах Максвелла. При этом Максвелл выдвинул важную идею, согласно которой должна существовать «симметрия» во взаимозависимости электрического и магнитного поля. То есть, если переменное во времени магнитное поле создает вихревое электрическое поле, можно ожидать, что и меняющееся во времени электрическое поле должно порождать магнитное поле.
Действительно, электрическое поле создается двумя способами: зарядами (так создается кулоновское поле) и изменяющимся во времени магнитным полем (так создается индукционное поле). Однако до сих пор упоминался лишь один способ возникновения магнитного поля ‑ посредством тока. Поэтому естественно предположить, что и для магнитного поля должен существовать второй способ его возникновения.
Рассмотрим еще раз закон полного тока, определяющий циркуляцию магнитного поля,
,
где и – сила результирующего макротока и микротока, соответственно, сквозь поверхность, образованную замкнутым контуром .
Максвелл обобщил закон полного тока. Согласно его гипотезе, кроме токов (макротоков в проводниках и микротоков в магнетиках), должна существовать еще одна причина возникновения магнитного поля. С целью иллюстрации рассуждений Максвелла, рассмотрим предложенный им мысленный эксперимент.
Если в данной цепи (рис. 5.1) замкнуть ключ, то лампа при постоянном токе гореть не будет, поскольку емкость C – разрывает цепь постоянного тока. Но в моменты включения лампа будет вспыхивать.
Если в предложенной электрической цепи включить источник переменного тока – лампа будет гореть, но в то же время ясно, что электроны с одной обкладки на другую не переходят, поскольку между ними изолятор (или вакуум). С другой стороны с помощью соответствующего прибора, измеряющего магнитное поле, можно обнаружить, что в промежутке между обкладками существует магнитное поле (рис. 5.2).
Рис. 5.2. Иллюстрация возникновения тока смещения
Для установления количественных соотношений между изменяющимся электрическим полем и вызываемым им магнитным полем Максвелл ввел в рассмотрение ток смещения. Максвелл определил плотность тока смещения в виде:
,
где ‑ вектор электрического смещения (именно название этого вектора дало название току смещения).
Теперь сумму тока проводимости и тока смещения можно назвать полным током. Его плотность:
.
Несмотря на кажущуюся общность, ток смещения эквивалентен току проводимости только в отношении способности создавать магнитное поле. Токи смещения существуют лишь там, где меняется со временем электрическое поле. В диэлектриках ток смещения состоит из двух существенно различных слагаемых. Поскольку вектор смещения равен , то отсюда видно, что плотность тока смещения складывается из «истинного» тока смещения и тока поляризации ‑ величины, обусловленной движением связанных зарядов. Очевидно, токи поляризации должны возбуждать магнитное поле, поскольку по своей природе эти токи не отличаются от токов проводимости. Самое «интересное» физическое свойство заключено в слагаемом , которое не связано ни с каким движением зарядов, а обусловлено только изменением электрического поля. Другими словами, даже в вакууме всякое изменение во времени электрического поля возбуждает в окружающем пространстве магнитное поле. Ток смещения в вакууме не выделяет джоулева тепла. Ток поляризации выделяет теплоту, связанную с трением в процессе поляризации диэлектрика.
Открытие Максвеллом тока смещения является чисто теоретическим выводом, однако данное открытие по своей значимости для физики аналогично открытию электромагнитной индукции Фарадеем.
77.243.189.99 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Что такое ток смещения
Если замкнуть ключ (рис. 6.1), то лампа при постоянном токе гореть не будет: емкость C – разрывает цепь постоянного тока. Но вот в моменты включения лампа будет вспыхивать.
При переменном токе – лампа горит, но в то же время нам ясно, что электроны из одной обкладки в другую не переходят – между ними изолятор (или вакуум). А вот если бы взять прибор, измеряющий магнитное поле, то в промежутке между обкладками мы обнаружили бы магнитное поле (рис. 7.2).
Для установления количественных соотношений между изменяющимся электрическим полем и вызываемым им магнитным полем Максвелл ввел в рассмотрение ток смещения. Этот термин имеет смысл в таких веществах, как, например, диэлектрики. Там смещаются заряды под действием электрического поля. Но в вакууме зарядов нет – там смещаться нечему, а магнитное поле есть. То есть название Максвелла «ток смещения» – не совсем удачное, но смысл, вкладываемый в него Максвеллом, – правильный.
Максвелл сделал вывод: всякое переменное электрическое поле порождает переменное магнитное поле.
Токи проводимости в проводнике замыкаются токами смещения в диэлектрике или в вакууме. Переменное электрическое поле в конденсаторе создает такое же магнитное поле, как если бы между обкладками существовал ток проводимости, имеющий величину, равную току в металлическом проводнике.
Это утверждение позволяет (на базе нашего примера с конденсатором) найти величину тока смещения. В свое время мы с вами доказали, что поверхностная плотность поляризационных зарядов σ равна – вектору электрического смещения:
Ток смещения
Согласно Максвеллу, если всякое переменное магнитное поле возбуждает в окружающем пространстве вихревое электрическое поле, то должно существовать и обратное явление: переменное электрическое поле должно вызывать появление в окружающем пространстве вихревого магнитного поля (второе основное положение теории Максвелла). Так как магнитное поле есть основной обязательный признак всякого тока, то Максвелл назвал переменное электрическое поле током смещения, в отличие от тока проводимости, обусловленного движением заряженных частиц (электронов и ионов).
Понятие тока смещения можно пояснить при помощи следующего опыта. Представим себе цепь переменного тока, содержащую конденсатор. Для суждения о наличии тока в контуре включим последовательно с конденсатором небольшую лампочку накаливания, играющую роль демонстрационного амперметра. Если бы контур был подключен к источнику постоянного тока, то через такой разомкнутый конденсатором контур постоянный ток не проходит и при длительном включении источника лампочка не обнаруживает никакого накала (лампочка кратковременно будет вспыхивать только в момент подключения источника). При подключении контура в осветительную цепь переменного тока (частотой 50 Гц) перезарядки конденсатора будут следовать непрерывно друг за другом с частотой 100 раз в секунду, и в контуре длительно будет существовать переменный ток. В этом случае отдельные вспышки лампочки уже не будут заметны, и лампочка будет накаливаться равномерно.
Можно отметить, что, в отличие от постоянного тока, переменные токи могут существовать и в разомкнутых контурах. При этом всякий раз, когда в разомкнутом контуре имеется ток, между его концами (между обкладками конденсатора) имеется изменяющееся во времени электрическое поле или ток смещения. Таким образом, токи проводимости в металлическом проводнике замыкаются токами смещения в диэлектрике.
Согласно Максвеллу электрическое поле в конденсаторе в любой момент времени создает такое же магнитное поле, как если бы между обкладками существовал ток проводимости с силой, равной силе тока в металлических проводах. Или, иными словами, магнитное поле нашего разомкнутого контура оказывается таким же, как если бы контур был замкнут.
Это позволяет найти количественную связь между изменяющимся электрическим полем и вызываемым им магнитным полем. Напряженность поля между обкладками плоского конденсатора согласно (6.5) равна E = s/e, но если пространство между обкладками заполнено диэлектриком с проницаемостью e, то напряженность в соответствии с (8.6) будет в e раз меньше, т.е.
Согласно (9.1) электрическое смещение D и напряженность поля Е связаны соотношением
где под s подразумевается модуль поверхностной плотности заряда.
Сравнивая выражения (41.1) и (41.2), находим, что электрическое смещение D в конденсаторе равно поверхностной плотности заряда s на обкладках:
Поэтому полный заряд q на каждой из обкладок равен:
где S – площадь обкладок.
Если за время dt заряд конденсатора изменяется на dq, то сила тока в проводе равна
I = = S .
Она однозначно связана с быстротой изменения электрического смещения (индукции электрического поля). Отсюда следует, что меняющееся поле конденсатора вызывает такое же магнитное поле, как ток, имеющий силу S×dD/dt или плотность тока
. (41.4)
Эта величина получила название плотности тока смещения.
Пользуясь этим понятием, можно второе положение Максвелла сформулировать в следующем виде: переменное во времени электрическое поле вызывает такое же магнитное поле, как и ток проводимости с плотностью , определяемый формулой (41.4).
В общем случае электрическое поле может быть неоднородным и может зависеть не только от времени, но и от координат. В этом случае выражение для плотности тока смещения будет
= , (41.5)
где знак частной производной указывает на то, что магнитное поле зависит от быстроты изменения индукции электрического поля во времени в каждой точке поля.
Следует подчеркнуть, что ток смещения определяется производной вектора , но не самим этим вектором.
Подчеркнем, что термин «ток смещения» является чисто условным. По существу ток смещения – это изменяющееся со временем электрическое поле. Основанием для того, чтобы назвать «плотностью тока» величину (41.5), служит лишь то, что размерность этой величины совпадает с размерностью плотности тока. Из всех физических свойств, присущих действительному току, ток смещения обладает лишь одним – способностью создавать магнитное поле.
Если в каком-либо проводнике имеется переменный ток, то внутри проводника существует переменное электрическое поле. Поэтому внутри проводника имеются и ток проводимости, и ток смещения, и магнитное поле проводника определяется их суммой, т.е. полным током. Плотность полного тока
= + . (41.6)
В зависимости от электропроводности среды и быстроты изменения поля (частоты переменного тока) оба слагаемых в (41.6) играют разную роль. В хорошо проводящих веществах (металлах) и при низких частотах плотность тока смещения мала, и током смещения можно пренебречь по сравнению с током проводимости. Напротив, в плохо проводящих средах (изоляторах) и при высоких частотах ток смещения играет основную роль.
Оба члена в формуле (41.6) могут иметь и одинаковые знаки и противоположные. Поэтому полный ток может быть как больше, так и меньше тока проводимости и в частном случае может обращаться в нуль.
Такой пример приведен на рисунке 53, где изображен сферический конденсатор, заполненный проводящей средой. Если заряд обкладок есть q, то электрическое смещение D на расстоянии R от центра равна
Плотность тока смещения равна
Jсм = ,
а сила тока смещения равна
Iсм = 4pR 2 Jсм = .
При разряде конденсатора этот ток направлен от внутренней обкладки к наружной. Ток же проводимости направлен противоположно (от плюса к минусу) и его сила есть
I = – .
Поэтому полный ток
и, несмотря на движение зарядов между обкладками, магнитное поле равно нулю.
Таким образом, в общем случае меняющихся токов магнитное поле определяется не током проводимости, а полным током. Если мы имеем разомкнутый контур, то на концах проводника обрывается лишь ток проводимости. В диэлектрике же между концами проводника имеется ток смещения, который замыкает ток проводимости. Поэтому, если под электрическим током понимать полный ток, определяемый формулой (41.6), то окажется, что в природе все электрические токи замкнуты. Этот важный вывод также был получен Максвеллом.
Максвелл обобщил теорему о циркуляции вектора (см. (36.9)), введя в ее правую часть полный ток Iполн = сквозь поверхность S, натянутую на замкнутый контур L. Тогда обобщенная теорема о циркуляции вектора запишется в виде
= Iполн = . (41.7)
Выражение (41.7) справедливо всегда, свидетельством чего является полное соответствие теории и опыта.
Источники:
http://studopedia.ru/3_183345_tok-smeshcheniya.html
http://ens.tpu.ru/posobie_fis_kusn/%D0%AD%D0%BB%D0%B5%D0%BA%D1%82%D1%80%D0%BE%D0%BC%D0%B0%D0%B3%D0%BD%D0%B5%D1%82%D0%B8%D0%B7%D0%BC/07-2.htm
http://mylektsii.ru/3-12479.html