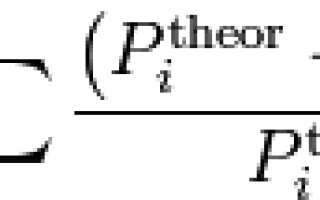Что такое критерий Пирсона

Критерий Пирсона

Критерий Пирсона, или критерий χ 2 — наиболее часто употребляемый критерий для проверки гипотезы о законе распределения. Во многих практических задачах точный закон распределения неизвестен, то есть является гипотезой, которая требует статистической проверки.

Обозначим через X исследуемую случайную величину. Пусть требуется проверить гипотезу H о том, что эта случайная величина подчиняется закону распределения F(x) . Для проверки гипотезы произведём выборку, состоящую из n независимых наблюдений над случайной величиной X. По выборке можно построить эмпирическое распределение F * (x) исследуемой случайной величины. Сравнение эмпирического F * (x) и теоретического распределений производится с помощью специально подобранной случайной величины — критерия согласия. Одним из таких критериев и является критерий Пирсона.

Содержание

Статистика критерия

Для проверки критерия вводится статистика:

где — предполагаемая вероятность попадения в i -й интервал, — соответствующее эмпирическое значение, n_i — число элементов выборки из i -го интервала.

Эта величина в свою очередь является случайной (в силу случайности X) и должна подчиняться распределению χ 2 .

Правило критерия

Перед тем, как сформулировать правило принятия или отвержения гипотезы необходимо учесть, что критерий Пирсона обладает правосторонней критической областью.

Литература

• Кендалл М., Стьюарт А. Статистические выводы и связи. — М.: Наука, 1973.

См. также

Wikimedia Foundation . 2010 .

Смотреть что такое “Критерий Пирсона” в других словарях:

Критерий согласия Пирсона — Критерий Пирсона, или критерий χ² (Хи квадрат) наиболее часто употребляемый критерий для проверки гипотезы о законе распределения. Во многих практических задачах точный закон распределения неизвестен, то есть является гипотезой, которая… … Википедия

Критерий согласия Колмогорова — или Критерий согласия Колмогорова Смирнова статистический критерий, использующийся для определения того, подчиняются ли два эмпирических распределения одному закону, либо того, подчиняется ли полученное распределение предполагаемой модели.… … Википедия

Критерий Вальда — (максиминный критерий[1]) один из критериев принятия решений в условиях неопределённости. Критерий крайнего пессимизма. История Критерий Вальда был предложен Абрахамом Вальдом в 1955 году для выборок равного объема, а затем распространен на … Википедия

Критерий Краскела — Уоллиса предназначен для проверки равенства медиан нескольких выборок. Данный критерий является многомерным обобщением критерия Уилкоксона Манна Уитни. Критерий Краскела Уоллиса является ранговым, поэтому он инвариантен по отношению к любому… … Википедия

Критерий Фишера — (F критерий, φ* критерий, критерий наименьшей значимой разности) апостериорный статистический критерий, используемый для сравнения дисперсий двух вариационных рядов, то есть для определения значимых различий между групповыми средними в… … Википедия

Критерий Кохрена — Критерий Кохрена используют при сравнении трёх и более выборок одинакового объёма . Расхождение между дисперсиями считается случайным при выбранном уровне значимости , если: где квантиль случайной величины при числе суммируемых… … Википедия

Критерий Лиллиефорса — статистический критерий, названный по имени Хьюберта Лиллиефорса, профессора статистики Университета Джорджа Вашингтона, являющийся модификацией критерия Колмогорова–Смирнова. Используется для проверки нулевой гипотезы о том, что выборка… … Википедия

Критерий Уилкоксона — Для улучшения этой статьи желательно?: Найти и оформить в виде сносок ссылки на авторитетные источники, подтверждающие написанное. Добавить иллюстрации. Т Крит … Википедия

Критерий Колмогорова — В статистике критерий согласия Колмогорова (также известный, как критерий согласия Колмогорова Смирнова) используется для того, чтобы определить, подчиняются ли два эмпирических распределения одному закону, либо определить, подчиняется ли… … Википедия

критерий независимости — для таблиц сопряженности проверяет гипотезу о том, что переменные строки и столбца независимы. К таким критериям относится критерий независимости хи квадрат (Пирсона) и точный критерий Фишера … Словарь социологической статистики

КРИТЕРИЙ ХИ-КВАДРАТ ПИРСОНА

​ Критерий χ 2 Пирсона – это непараметрический метод, который позволяет оценить значимость различий между фактическим (выявленным в результате исследования) количеством исходов или качественных характеристик выборки, попадающих в каждую категорию, и теоретическим количеством, которое можно ожидать в изучаемых группах при справедливости нулевой гипотезы. Выражаясь проще, метод позволяет оценить статистическую значимость различий двух или нескольких относительных показателей (частот, долей).

1. История разработки критерия χ 2

Критерий хи-квадрат для анализа таблиц сопряженности был разработан и предложен в 1900 году английским математиком, статистиком, биологом и философом, основателем математической статистики и одним из основоположников биометрики Карлом Пирсоном (1857-1936).

2. Для чего используется критерий χ 2 Пирсона?

Критерий хи-квадрат может применяться при анализе таблиц сопряженности, содержащих сведения о частоте исходов в зависимости от наличия фактора риска. Например, четырехпольная таблица сопряженности выглядит следующим образом:

Как заполнить такую таблицу сопряженности? Рассмотрим небольшой пример.

Проводится исследование влияния курения на риск развития артериальной гипертонии. Для этого были отобраны две группы исследуемых – в первую вошли 70 человек, ежедневно выкуривающих не менее 1 пачки сигарет, во вторую – 80 некурящих такого же возраста. В первой группе у 40 человек отмечалось повышенное артериальное давление. Во второй – артериальная гипертония наблюдалась у 32 человек. Соответственно, нормальное артериальное давление в группе курильщиков было у 30 человек (70 – 40 = 30) а в группе некурящих – у 48 (80 – 32 = 48).

Заполняем исходными данными четырехпольную таблицу сопряженности:

В полученной таблице сопряженности каждая строчка соответствует определенной группе исследуемых. Столбцы – показывают число лиц с артериальной гипертонией или с нормальным артериальным давлением.

Задача, которая ставится перед исследователем: имеются ли статистически значимые различия между частотой лиц с артериальным давлением среди курящих и некурящих? Ответить на этот вопрос можно, рассчитав критерий хи-квадрат Пирсона и сравнив получившееся значение с критическим.

3. Условия и ограничения применения критерия хи-квадрат Пирсона

1. Сопоставляемые показатели должны быть измерены в номинальной шкале (например, пол пациента – мужской или женский) или в порядковой (например, степень артериальной гипертензии, принимающая значения от 0 до 3).
2. Данный метод позволяет проводить анализ не только четырехпольных таблиц, когда и фактор, и исход являются бинарными переменными, то есть имеют только два возможных значения (например, мужской или женский пол, наличие или отсутствие определенного заболевания в анамнезе. ). Критерий хи-квадрат Пирсона может применяться и в случае анализа многопольных таблиц, когда фактор и (или) исход принимают три и более значений.
3. Сопоставляемые группы должны быть независимыми, то есть критерий хи-квадрат не должен применяться при сравнении наблюдений “до-“после”. В этих случаях проводится тест Мак-Немара (при сравнении двух связанных совокупностей) или рассчитывается Q-критерий Кохрена (в случае сравнения трех и более групп).
4. При анализе четырехпольных таблиц ожидаемые значения в каждой из ячеек должны быть не менее 10. В том случае, если хотя бы в одной ячейке ожидаемое явление принимает значение от 5 до 9, критерий хи-квадрат должен рассчитываться с поправкой Йейтса. Если хотя бы в одной ячейке ожидаемое явление меньше 5, то для анализа должен использоваться точный критерий Фишера.
5. В случае анализа многопольных таблиц ожидаемое число наблюдений не должно принимать значения менее 5 более чем в 20% ячеек.

4. Как рассчитать критерий хи-квадрат Пирсона?

Для расчета критерия хи-квадрат необходимо:

Рассчитываем ожидаемое количество наблюдений для каждой из ячеек таблицы сопряженности (при условии справедливости нулевой гипотезы об отсутствии взаимосвязи) путем перемножения сумм рядов и столбцов с последующим делением полученного произведения на общее число наблюдений. Общий вид таблицы ожидаемых значений представлен ниже:

Критерий согласия Пирсона

Критерий согласия Пирсона

1. Услуги проектирования
2. Теория вероятности [Калинин В.М., Тихомиров С.Р.]
3. Критерий согласия Пирсона

Критерий согласия Пирсона

Опр Критерий проверки гипотезы о предполагаемом законе неизвестного распределения называется критерием согласия.

Имеется несколько критериев согласия: $chi ^2$ < хи-квадрат >К. Пирсона, Колмогорова, Смирнова и др.

Обычно теоретические и эмпирические частоты различаются. Случай расхождения может быть не случайным, значит и объясняется тем, что не верно выбрана гипотеза. Критерий Пирсона отвечает на поставленный вопрос, но как любой критерий он ничего не доказывает, а лишь устанавливает на принятом уровне значимости её согласие или несогласие с данными наблюдений.

Опр Достаточно малую вероятность, при которой событие можно считать практически невозможным называют уровнем значимости.

На практике обычно принимают уровни значимости, заключённые между 0,01 и 0,05, $alpha =0,05$ – это $5 < % >$ уровень значимости.

В качестве критерия проверки гипотезы примем величину begin label < eq1 >chi ^2=sum < frac < ( < n_i -n_i' >)^2 > < n_i' >> qquad (1) end

здесь $n_i -$ эмпирические частоты, полученные из выборки, $n_i’ -$ теоретические частоты, найденные теоретическим путём.

Доказано, что при $nto infty $ закон распределения случайной величины < 1 >независимо от того, по какому закону распределена генеральная совокупность, стремится к закону $chi ^2$ < хи-квадрат >с $k$ степенями свободы.

Опр Число степеней свободы находят по равенству $k=S-1-r$ где $S-$ число групп интервалов, $r-$ число параметров.

1) равномерное распределение: $r=2, k=S-3 $

2) нормальное распределение: $r=2, k=S-3 $

3) показательное распределение: $r=1, k=S-2$.

Правило. Проверка гипотезы по критерию Пирсона.

1. Для проверки гипотезы вычисляют теоретические частоты и находят $chi _ < набл >^2 =sum < frac < ( < n_i -n_i' >)^2 >< n_i' >> $
2. По таблице критических точек распределения $chi ^2$ по заданному уровню значимости $alpha $ и числу степеней свободы $k$ находят $chi _ < кр >^2 ( < alpha ,k >)$.
3. Если $chi _ < набл >^2

Проверка гипотезы о равномерном распределении

Функция плотности равномерного распределения величины $X$ имеет вид $f( x )=frac < 1 > < b-a >xin left[ < a,b >right]$.

Для того, чтобы при уровне значимости $alpha $ проверить гипотезу о том, что непрерывная случайная величина распределена по равномерному закону, требуется:

1) Найти по заданному эмпирическому распределению выборочное среднее $overline < x_b >$ и $sigma _b =sqrt < D_b >$. Принять в качестве оценки параметров $a$ и $b$ величины

$a = overline x _b -sqrt 3 sigma _b $, $b = overline x _b +sqrt 3 sigma _b $

2) Найти вероятность попадания случайной величины $X$ в частичные интервалы $( < x_i ,x_ < i+1 >> )$ по формуле $ P_i =P( < x_i

Источники:

https://dic.academic.ru/dic.nsf/ruwiki/989265
https://medstatistic.ru/theory/hi_kvadrat.html
https://3dstroyproekt.ru/teorija-verojatnosti/kriterij-soglasija-pirsona