Что такое эффект Комптона

Эффект Комптона

Как мы знаем, Альберт Эйнштейн в 1905 году предложил для объяснения фотоэффекта так называемую концепцию фотонов. Позже, в 1922 г., американский физик А.Комптон провел серию опытов и подтвердил ее экспериментально. Он провел исследования упругого рассеяния коротковолнового рентгеновского излучения на свободных электронах вещества (или электронах, слабо связанных с атомами) и открыл, что длина волны рассеянного изучения не соответствует ранее принятой волновой теории. Согласно ей, электроны, испытывающие воздействие периодического поля световой волны, совершают вынужденные колебания на частоте волны и поэтому излучают рассеянные волны той же частоты, следовательно, длина волны излучения при рассеянии не должна меняться.

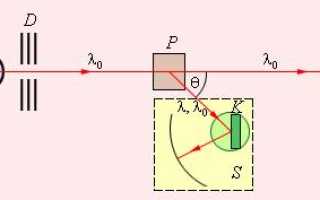
На иллюстрации представлена схема прохождения монохроматического рентгеновского излучения с длиной волны λ 0 , которое исходит из трубки R , через свинцовую диафрагму. После прохождения его направляют узким пучком на слой рассеивающего вещества (алюминия, графита). Затем получившееся излучение, рассеянное под углом θ , анализируют при помощи спектрографа рентгеновских лучей S с дифракционной решеткой в виде кристалла K , помещенного на поворотный столик. Результаты опыта показывают, что в рассеянном излучении длина волны Δ λ увеличивается в зависимости от угла рассеяния.

∆ λ = λ – λ 0 = 2 Λ sin 2 θ 2 .

Здесь параметр Λ = 2 , 43 · 10 – 3 н м выражает так называемую комптоновскую длину волны, которая не имеет связи с свойствами рассеивающего вещества.

Если излучение является рассеянным, то в нем помимо спектральной линии с длиной волны λ присутствует и несмещенная линия, длина волны которой равна λ 0 .

Соотношение интенсивности обеих линий связано с тем, какое вещество использовано в качестве рассеивающего.

Рисунок 5 . 3 . 1 . Эксперимент Комптона (схематическое изображение).

Следующие иллюстрации показывают, как распределяется интенсивность в спектре рассеянного излучения в зависимости от угла рассеивания.

Рисунок 5 . 3 . 2 . Распределение интенсивности в рассеянном излучении.

Объяснение эффекта с помощью квантовых представлений

Эффект Комптона был объяснен в 1923 году самим Комптоном и П. Дебаем, которые работали независимо друг от друга. В обоих случаях в основе объяснения лежат квантовые представления.

Если излучение является потоком фотонов, то эффект Комптона происходит из-за упругого столкновения свободных электронов вещества с рентгеновскими фотонами. Рассеивающие вещества имеют слабую связь между ядрами атомов и электронами, поэтому можно считать, что они имеют в составе свободные электроны. При столкновении им передается часть энергии фотонов и часть импульса.

Рассмотрим подробнее процесс упругого столкновения налетающего фотона с импульсом p 0 = h ν 0 c и энергией E 0 = h ν 0 с электроном, у которого энергия покоя составляет E e 0 = m c 2 . После того, как частицы столкнутся, направление движения фотона изменяется, т.е. происходит рассеяние, после чего импульс фотона становится равен p = h ν c , а энергия – E = h ν E 0 . Что касается электрона, то, согласно релятивистской формуле, его энергия становится равной E e = p e 2 c 2 + m 2 c 4 (буквой p e обозначен приобретенный импульс). Запишем формулу закона сохранения:

E + E e 0 = E + E e .

Иначе говоря, h υ 0 + m c 2 = h υ + p e 2 c 2 + m 2 c 4 .

Также нам понадобится закон сохранения импульса:

С помощью теоремы косинусов мы можем перевести его в скалярную форму:

p e 2 = h υ 0 c 2 + h υ c 2 – 2 h 2 c 2 υ 0 υ cos θ .

Рисунок 5 . 3 . 3 . Распределение импульсов при столкновении налетающего фотона и покоящегося электрона

Теперь возьмем эти два соотношения (законы сохранения импульса и энергии), проведем несложные преобразования, исключив p e , и получим следующее:

m c 2 υ 0 – υ = h υ 0 υ ( 1 – cos θ ) .

Перейдем от частот к волнам υ 0 = c λ 0 , υ = c λ . У нас получится выражение, совпадающее с формулой Комптона, которая была получена при эксперименте:

∆ λ = λ – λ 0 = h m c ( 1 – cos θ ) = 2 h m c sin 2 θ 2 .

Проведенные теоретические расчеты, использующие квантовые представления, помогают не только объяснить эффект Комптона, но и вывести формулу нахождения длины волны с помощью фундаментальных констант m , h , c :

Λ = h m c = 2 , 426 · 10 – 3 н м .

Почему длина части волн не изменяется?

Согласно данным опыта, в излучении после рассеяния кроме смещенной линии есть и несмещенная, длина волны излучения которой совпадает с первоначальной. Ее наличие можно объяснить тем, что часть фотонов взаимодействует с электронами, крепко связанными с ядрами атомов. Тогда происходит обмен энергии и импульса с атомом в целом, а не только с электроном. Поскольку атом весит значительно больше, то переданная энергия фотона очень мала, следовательно, длина волны λ рассеянного излучения остается практически неизменной.

Рисунок 5 . 3 . 4 . Модель комптоновского рассеяния.

Комптона эффект

Большая советская энциклопедия. — М.: Советская энциклопедия . 1969—1978 .

Смотреть что такое “Комптона эффект” в других словарях:

КОМПТОНА ЭФФЕКТ — (комптон эффект), упругое рассеяние эл. магн. излучения на свободных (или слабо связанных) эл нах, сопровождающееся увеличением длины волны; наблюдается при рассеянии излучения малых длин волн рентгеновского и g излучений. Открыт в 1922 амер.… … Физическая энциклопедия

КОМПТОНА ЭФФЕКТ — открытое А. Комптоном (1922) упругое рассеяние электромагнитного излучения малых длин волн (рентгеновского и гамма излучения) на свободных электронах, сопровождающееся увеличением длины волны l. Комптона эффект противоречит классической теории,… … Большой Энциклопедический словарь

Комптона эффект — Квантовая механика Принцип неопределённости Введение . Математическая формулировка . Основа … Википедия

Комптона эффект — открытое А. Комптоном (1922) упругое рассеяние электромагнитного излучения малых длин волн (рентгеновского и гамма излучения) на свободных электронах, сопровождающееся увеличением длины волны λ. Комптона эффект противоречит классической теории,… … Энциклопедический словарь

КОМПТОНА ЭФФЕКТ — изменение длины волны, сопровождающее рассеяние пучка рентгеновских лучей в тонком слое вещества. Явление было известно еще за несколько лет до работы А. Комптона, который опубликовал в 1923 результаты тщательно выполненных экспериментов,… … Энциклопедия Кольера

Комптона эффект — (А. Н. Compton, 1892 1962, амер. физик) рассеяние энергии электромагнитного излучения на свободных или слабо связанных электронах; К. э. обусловливает ослабление рентгеновского или гамма излучения при прохождении через ткани организма … Большой медицинский словарь

КОМПТОНА ЭФФЕКТ — открытое А. Комптоном (1922) упругое рассеяние зл. магн. излучения малых длин волн (рентгеновского и гамма излучения) на свободных электронах, сопровождающееся увеличением длины волны Л. К. э. противоречит классич. теории, согласно к рой при… … Естествознание. Энциклопедический словарь

КОМПТОНА ЭФФЕКТ ОБРАТНЫЙ — упругое рассеяние фотонов на электронах высокой энергии, приводящее к увеличению энергии (частоты) фотонов (уменьшению длины волны) … Большой Энциклопедический словарь

комптона эффект обратный — упругое рассеяние фотонов на электронах высокой энергии, приходящее к увеличению энергии (частоты) фотонов (уменьшению длины волны). * * * КОМПТОНА ЭФФЕКТ ОБРАТНЫЙ КОМПТОНА ЭФФЕКТ ОБРАТНЫЙ, упругое рассеяние фотонов на электронах высокой энергии … Энциклопедический словарь

КОМПТОНА ЭФФЕКТ ОБРАТНЫЙ — упругое рассеяние фотонов на электронах высокой энергии, приводящее к увеличению энергии (частоты) фотонов (уменьшению длины волны) … Естествознание. Энциклопедический словарь

КО́МПТОНА ЭФФЕ́КТ

КО́МПТОНА ЭФФЕ́КТ (ком­пто­нов­ское рас­сея­ние), рас­сея­ние жё­ст­ко­го (ко­рот­ко­вол­но­во­го) элек­тро­маг­нит­но­го из­лу­че­ния на сво­бод­ных за­ря­жен­ных час­ти­цах, со­про­во­ж­даю­щее­ся из­ме­не­ни­ем дли­ны вол­ны рас­се­ян­но­го из­лу­че­ния. От­крыт А. Комп­то­ном в 1922 при рас­сея­нии жё­ст­ких рент­ге­нов­ских лу­чей в гра­фи­те, атом­ные элек­тро­ны ко­то­ро­го, рас­сеи­ваю­щие из­лу­че­ние, мо­гут с хо­ро­шей точ­но­стью рас­смат­ри­вать­ся как сво­бод­ные (по­сколь­ку час­то­та рент­ге­нов­ских лу­чей на­мно­го пре­вос­хо­дит ха­рак­тер­ные час­то­ты дви­же­ния элек­тро­нов в лёг­ких ато­мах). Со­глас­но из­ме­ре­ни­ям Ком­пто­на, пер­во­на­чаль­ная дли­на вол­ны рент­ге­нов­ско­го из­лу­че­ния $λ_0 $ при рас­сея­нии его на угол $theta$ уве­ли­чи­ва­лась и ока­зы­ва­лась рав­ной $λ′=λ_0+λ_C (1-cos theta) tag 1, $ где $λ_C$ – по­сто­ян­ная для всех ве­ществ ве­ли­чи­на, на­зван­ная ком­пто­нов­ской дли­ной вол­ны элек­тро­на. (Бо­лее час­то упот­реб­ля­ет­ся ве­ли­чи­на $barlambda_C$ = $λ/2π=3,86159268·10^ <–11>$ см.) К. э. рез­ко про­ти­во­ре­чит клас­сич. вол­но­вой тео­рии све­та, со­глас­но ко­то­рой дли­на вол­ны элек­тро­маг­нит­но­го из­лу­че­ния не долж­на ме­нять­ся при его рас­сея­нии на сво­бод­ных элек­тро­нах. По­это­му от­кры­тие К. э. яви­лось од­ним из важ­ней­ших фак­тов, ука­зав­ших на двой­ст­вен­ную при­ро­ду све­та (см. Кор­пус­ку­ляр­но-вол­но­вой дуа­лизм ). Объ­яс­не­ние эф­фек­та, дан­ное Ком­пто­ном и, не­за­ви­си­мо от него, П. Де­ба­ем , за­клю­ча­ет­ся в том, что $gamma$ -квант с энер­ги­ей $ℰ=ℏω$ и им­пуль­сом $boldsymbol p=ℏ boldsymbol k$ , стал­ки­ва­ясь с элек­тро­ном, пе­ре­да­ёт ему в за­ви­си­мо­сти от уг­ла рас­сея­ния часть сво­ей энер­гии. (Здесь $hbar$ – по­сто­ян­ная План­ка, $omega$ – цик­ли­че­ская час­то­та элек­тро­маг­нит­ной вол­ны, $boldsymbol k$ – её вол­но­вой век­тор $boldsymbol<|k|>=omega/c$ , свя­зан­ный с дли­ной вол­ны со­от­но­ше­ни­ем $lambda= 2pi / boldsymbol <|k|>$ .) Со­глас­но за­ко­нам со­хра­не­ния энер­гии и им­пуль­са, энер­гия $γ$ -кван­та, рас­се­ян­но­го на по­коя­щем­ся элек­тро­не, рав­на $$ℰ’=frac<ℰ><1+ℰ/mc^2(1-cos theta)>, tag 2 $$ что пол­но­стью со­от­вет­ст­ву­ет дли­не вол­ны рас­се­ян­но­го из­лу­че­ния $λ′$ . При этом ком­пто­нов­ская дли­на вол­ны элек­тро­на вы­ра­жа­ет­ся че­рез фун­дам. по­сто­ян­ные: мас­су элек­тро­на $m_e$ , ско­рость све­та с и по­сто­ян­ную План­ка $hbar:barlambda_C=hbar/m_ec$ . Пер­вым ка­че­ст­вен­ным под­твер­жде­ни­ем та­кой ин­тер­пре­та­ции К. э. бы­ло на­блю­де­ние в 1923 Ч. Т. Р. Виль­со­ном элек­тро­нов от­да­чи при об­лу­че­нии воз­ду­ха рент­ге­нов­ски­ми лу­ча­ми в изо­бре­тён­ной им ка­ме­ре (ка­ме­ре Виль­со­на). Под­роб­ные ко­ли­че­ст­вен­ные ис­сле­до­ва­ния К. э. бы­ли про­ве­де­ны Д. В. Ско­бель­цы­ным , ис­поль­зо­вав­шим в ка­че­ст­ве ис­точ­ни­ка γ -кван­тов вы­со­ких энер­гий ра­дио­ак­тив­ный пре­па­рат RaC ( 214 Bi), а в ка­че­ст­ве де­тек­то­ра – ка­ме­ру Виль­со­на, по­ме­щён­ную в маг­нит­ное по­ле. Дан­ные Ско­бель­цы­на бы­ли в даль­ней­шем ис­поль­зо­ва­ны для про­вер­ки кван­то­вой элек­тро­ди­на­ми­ки. В ре­зуль­та­те этой про­вер­ки швед. фи­зик О. Клейн, япон. фи­зик Й. Ни­ши­на и И. Е. Тамм уста­но­ви­ли, что эф­фек­тив­ное се­че­ние К. э. убы­ва­ет с рос­том энер­гии γ -кван­тов (т. е. с умень­ше­ни­ем дли­ны вол­ны элек­тро­маг­нит­но­го из­лу­че­ния), а при дли­нах волн, зна­чи­тель­но пре­вы­шаю­щих ком­пто­нов­скую, стре­мит­ся к пре­де­лу $sigma_T=(8pi/3)r_e^2=0, 6652459cdot 10^<24>$ см 2 , ука­зан­но­му Дж. Дж. Том­со­ном на ос­но­ве вол­но­вой тео­рии ( $r_e=e^2/m_ec^2 $ — клас­сич. ра­ди­ус элек­тро­на).

Источники:

https://zaochnik.com/spravochnik/fizika/kvantovaja-fizika/effekt-komptona/
https://dic.academic.ru/dic.nsf/bse/97575/%D0%9A%D0%BE%D0%BC%D0%BF%D1%82%D0%BE%D0%BD%D0%B0
https://bigenc.ru/physics/text/2087597