При каких условиях возникают свободные колебания

Свободные колебания.

Свободные колебания (или собственные колебания) — это колебания колебательной системы, совершаемые только благодаря первоначально сообщенной энергии (потенциальной или кинети­ческой) при отсутствии внешних воздействий.

Потенциальная или кинетическая энергия может быть сообщена, например, в механических системах через начальное смещение или начальную скорость.

Свободно колеблющиеся тела всегда взаимодействуют с другими телами и вместе с ними обра­зуют систему тел, которая называется колебательной системой.

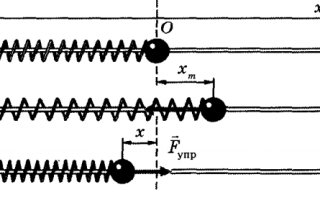
Например, пружина, шарик и вертикальная стойка, к которой прикреплен верхний конец пружины (см. рис. ниже), входят в колебательную систему. Здесь шарик свободно скользит по струне (силы трения пренебрежимо малы). Если отвести шарик вправо и предоставить его самому себе, он будет совершать свободные колебания около положения равновесия (точки О) вследствие действия силы упругости пружины, направленной к положению равновесия.

Другим классическим примером механической колебательной системы является математический маятник (см. рис. ниже). В данном случае шарик совершает свободные колебания под действием двух сил: силы тяжести и силы упругости нити (в колебательную систему входит также Земля). Их равнодействующая направлена к положению равновесия.

Силы, действующие между телами колебательной системы, называются внутренними силами. Внешними силами называют­ся силы, действующие на систему со стороны тел, не входящих в нее. С этой точки зрения свобод­ные колебания можно определить как колебания в системе под действием внутренних сил после того, как система выведена из положения равновесия.

Условиями возникновения свободных колебаний являются:

1) возникновение в них силы, возвращающей систему в положение устойчивого равновесия, после того как ее вывели из этого состояния;

2) отсутствие трения в системе.

Динамика свободных колебаний.

Колебания тела под действием сил упругости. Уравнение колебательного движения тела под действием силы упругости F (см. рис.) может быть получено с учетом второго закона Ньютона (F = mа) и закона Гука (F_упр = -kx), где m — масса шарика, а — ускорение, приобретаемое шариком под действием силы упругости, k — коэффициент жесткости пружины, х — смещение тела от положения равновесия (оба уравнения записаны в проекции на горизонтальную ось Ох). Приравнивая правые части этих уравнений и учитывая, что ускорение а — это вторая производная от координаты х (смещения), получим:

.

Это дифференциальное уравнение движения тела, колеблющегося под действием силы упругости: вторая производная координаты по времени (ускорение тела) прямо пропорциональна его координате, взятой с противоположным знаком.

Колебания математического маятника. Для получения уравнения колебания математического маятника (рисунок) необходимо разложить силу тяжести F_T = mg на нормальную F_n (направлен­ную вдоль нити) и тангенциальную F_τ (касательную к траектории движения шарика — окружности) составляющие. Нормальная составляющая силы тяжести F_n и сила упругости нити F_ynp в сумме сооб­щают маятнику центростремительное ускорение, не влияющее на величину скорости, а лишь меня­ющее ее направление, а тангенциальная составляющая F_τ является той силой, которая возвращает шарик в положение равновесия и заставляет его совершать колебательные движения. Используя, как и в предыдущем случае, закон Ньютона для тангенциального ускорения ma_τ = F_τ и учитывая, что F_τ = -mg sinα, получим:

Знак минус появился потому, что сила и угол отклонения от положения равновесия α име­ют противоположные знаки. Для малых углов отклонения sin α ≈ α. В свою очередь, α = s/l, где s — дуга OA, I — длина нити. Учитывая, что а_τ = s”, окончательно получим:

.

Вид уравнения аналогичен уравнению . Только здесь параметрами системы являются длина нити и ускорение свободного падения, а не жесткость пружины и масса шарика; роль координаты играет длина дуги (т. е. пройденный путь, как и в первом случае).

Таким образом, свободные колебания описываются уравнениями одного вида (подчиняются одним и тем же законам) независимо от физической природы сил, вызывающих эти колебания.

Решением уравнений и является функция вида:

То есть координата тела, совершающего свободные колебания, меняется с течением времени по закону косинуса или синуса, и, следовательно, эти колебания являются гармоническими:

В уравнении x = x_m cos ω t (или x = x_m sin ω t), х_m — амплитуда колебания, ω — собственная циклическая (круговая) частота колебаний.

Циклическая частота и период свободных гармонических колебаний определяются свойствами системы. Так, для колебаний тела, прикрепленного к пружине, справедливы соотношения:

.

Собственная частота тем больше, чем больше жесткость пружины или меньше масса груза, что вполне подтверждается опытом.

Для математического маятника выполняются равенства:

.

Эта формула была впервые получена и проверена на опыте голландским ученым Гюйгенсом (современником Ньютона).

Период колебаний возрастает с увеличением длины маятника и не зависит от его массы.

Следует особо обратить внимание на то, что гармонические колебания являются строго периодическими (т. к. подчиняются закону синуса или косинуса) и даже для математического маятни­ка, являющегося идеализацией реального (физического) маятника, возможны только при малых углах колебания. Если углы отклонения велики, смещение груза не будет пропорционально углу отклонения (синусу угла) и ускорение не будет пропорционально смещению.

Скорость и ускорение тела, совершающего свободные колебания, также будут совершать гармонические колебания. Беря производную по времени функции (x = x_m cos ω t (или x = x_m sin ω t)), получим выражение для скорости:

где a_m = ω 2 x_m — амплитуда ускорения. Таким образом, амплитуда скорости гармонических коле­баний пропорциональна частоте, а амплитуда ускорения — квадрату частоты колебания.

ПРи каких условиях возникает колебание?!

Поиск по вопросам
Наука, Техника, Языки
Гуманитарные науки
Естественные науки
Лингвистика
Техника
Вопросы-лидеры

Трансформатор не гудит, когда его ставишь вверх креплениями, а вниз – гудит, что такое, я не понимаю
1 ставка

Dna 250 не работает с 2 аккумуляторами
1 ставка
Лидеры категории
Аркаша
Искусственный Интеллект
U(CN)5
Гений
Владимир
Искусственный Интеллект
•••

Крутая онлайн-игра! 12+

Ничего не скачивай и не плати, играй бесплатно.
101xp.com
Создать персонажа? 12+

Множество уникальных персонажей в бесплатной онлайн игре. Ничего скачивать не нужно!
creagames.com
Обзор новых займов под 0% 18+

Уже 15 займов под 0%, 4 займа со скидкой, 10 займов без проверки КИ и 7 займов без отказа.
zaimini.ru
создать рекламу
при каких условиях возникают колебания
Владимир Булгаков Знаток (276), Вопрос решён 6 лет назад
1 Нравится
ЛУЧШИЙ ОТВЕТ
Maygli 6 лет назад
Просветленный (23918)
при резонансе
Нравится Пожаловаться
5 ОТВЕТОВ
Абрикос 6 лет назад
Мастер (1091)
Свободные колебания возникают в колебательной системе при следующих условиях:
1) силы трения в системе должны быть малы
2) силы ( или хотя бы одна из сил) , вызывающие колебания должны зависеть от координаты ( такой силой обычно является сила упругости)
3) систему нужно вывести из положения равновесия ( то есть привести в движение приложив кратковременную внешнюю силу)
Вообще колебания в системе происходят под действием силы тяжести и силы упругости.
2 Нравится Пожаловаться
target Реклама 12+

creagames.com
Создать персонажа?
Множество уникальных персонажей в бесплатной онлайн игре. Ничего скачивать не нужно!
Играть
creagames.com
Создать персонажа?
Множество уникальных персонажей в бесплатной онлайн игре. Ничего скачивать не нужно! Множество уникальных персонажей в бесплатной онлайн игре. Ничего скачивать не нужно! Множество уникальных персонажей в бесплатной онлайн игре. Ничего скачивать не нужно! Множество уникальных персонажей в бесплатной онлайн игре. Ничего скачивать не нужно!
Играть
Paweł 6 лет назад
Гений (56115)
Условия возникновения механических колебаний

1. Хотя бы одна сила должна зависеть от координат.
2. При выведении тела из положения устойчивого равновесия возникает равнодействующая, направленная к положению равновесия. С энергетической точки зрения это значит, что возникают условия для постоянного перехода кинетической энергии в потенциальную и обратно.
3. Силы трения в системе малы.

Поскольку между электромагнитными колебаниями и механическими есть прямая аналогия (вспомните формулы – всё одинаково, только буковки разные) , то можно и общие для всех колебаний условия сформулировать:
Система должна обладать:
1) устойчивым положением равновесия
2) инерционнымисвойствами;
3) малыми потерями энергии колебаний (на преодоление сил
трения в случае механических колебаний и на нагревание проводников в случае
электромагнитных колебаний в контуре)

Механические колебания

КОЛЕБАНИЯ

Колебания – процессы (изменения состояния), обладающие той или иной повторяемостью во времени.

Механические колебания – движения, которые точно или приблизительно повторяются во времени. Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени. (В противном случае колебания наз. апериодическими).

Примеры колебаний, изображенные на рисунках: колебания математического маятника, колебания жидкости в U-образной трубке, колебания тела под действием пружин, колебания натянутой струны.

Условия возникновения механических колебаний

1. Хотя бы одна сила должна зависеть от координат.
2. При выведении тела из положения устойчивого равновесия возникает равнодействующая, направленная к положению равновесия. С энергетической точки зрения это значит, что возникают условия для постоянного перехода кинетической энергии в потенциальную и обратно.
3. Силы трения в системе малы.

Для возникновения колебания тело необходимо вывести из положения равновесия, сообщив либо кинетическую энергию (удар, толчок), либо – потенциальную (отклонение тела).

Примеры колебательных систем:

1. Нить, груз, Земля.
2. Пружина, груз.
3. Жидкость в U-образной трубке, Земля.
4. Струна.

Свободные колебания — это колебания, которые возникают в системе под действием внутренних сил, после того как система была выведена из положения устойчивого равновесия. В реальной жизни все свободные колебания являются затухающими (т.е. их амплитуда, размах, уменьшается с течением времени).

Вынужденные колебания – колебания, которые происходят под действием внешней периодической силы.

Характеристики колебательного процесса.

1. Смещение х – отклонение колеблющейся точки от положе­ния равновесия в данный момент времени (м).

2. Амплитуда х_м – наибольшее смещение от положения рав­новесия (м). Если колебания незатухающие, то амплитуда постоянна.

3. Период Т — время, за которое совершается одно полное колебание. Выражается в секундах (с).

За время, равное одному периоду (одно полное колебание) тело совершает перемещение, равное 0 и проходит путь, равный 2πr.

4. Частота ν — число полных колебаний за единицу времени. В СИ измеряется в герцах (Гц).

Частота колебаний равна одному герцу, если за 1 секунду совершается 1 полное колебание. 1 Гц= 1 с -1 .

5. Циклической (круговой) частотой ω периодических колебаний наз. число полных колебаний, которые совершаются за 2π единиц времени (секунд). Единица измерения – с -1 .

6. Фаза колебания – φ – физическая величина, определяющая смещение x в данный момент времени. Измеряется в радианах (рад).

Фаза колебания в начальный момент времени (t=0) называется начальной фазой (φ).

Источники:

https://www.calc.ru/Svobodnyye-Kolebaniya.html
https://otvet.mail.ru/question/12035157
https://msk.edu.ua/ivk/Fizika/Konspekt/kolebania.php