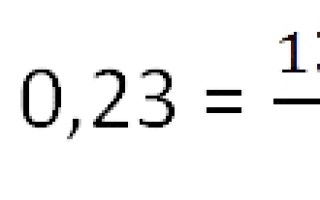Как правильно решать задачи на проценты

Простой процентный рост.

Если человек не вносит своевременную плату за квартиру, то на него налагается штраф, который называется «пеня». Так в Москве пеня составляет 1% от суммы квартплаты за каждый день просрочки. Поэтому, например, за 19 дней просрочки, сумма составит 19% от суммы квартплаты, и в месте , скажем, со 100 руб. квартплаты человек должен будет внести пеню 0,19 * 100 = 19 руб., а всего 119 руб.

Ясно, что в разных городах и у разных людей, квартплата, размер пани и время просрочки разные. Поэтому имеет смысл, составить общую формулу квартплаты для неаккуратных плательщиков, применимую при любых обстоятельствах.

Пусть S – ежемесячная кварт плата, пеня составляет p % квартплаты за каждый день просрочки, а n – число просроченных дней. Сумму, которую должен заплатить человек после n дней просрочки, обозначим S_n .

Тогда за n дней просрочки, пеня составит pn % от S , или pn:100*S , а всего придётся заплатить

Задача 1. Сколько надо заплатить москвичу, если его квартплата составляет 100 руб. и просрочена на 5 дней?

Подставляя в формулу значение p = 1 и значения n = 5 * 4, получим:

(1 + 1*5:100 ) * 100 = 1,05 * 100 = 105 (руб.)

Ответ: через 5 дней – 105 руб.

Таким образом, установленная формула позволяет быстро рассчитывать необходимые значения выплат за квартиру.

Рассмотрим еще одну ситуацию. Банк выплачивает вкладчикам каждый месяц p % от внесенной суммы. Поэтому, если клиент внес сумму S , то через n месяцев на его счете будет ( 1+pn:100 ) S , и мы вновь получаем, что

Мы получили в точности ту же самую формулу, что и в примере с квартплатой, хотя буквы в этих двух примерах имеют разный смысл: в первом примере n – число дней, а во втором примере n – число месяцев, в первом примере S – величина квартплаты, а во втором S – сумма, внесенная в банк. Такая же формула будет получаться и во всех иных случаях, когда некоторая величина увеличивается на постоянное число процентов за каждый фиксированный период времени. Эта формула описывает многие конкретные ситуации и имеет специальное название: формула простого процентного роста.

Задача 2. Банк выплачивает вкладчикам каждый месяц 2% от внесённой суммы. Клиент сделал вклад в размере 500 рублей. Какая сумма будет на его счёте через полгода?

Для решения задачи достаточно подставить в формулу величину процентной ставки p = 2, числа месяцев n = 6 и первоначального вклада S = 500:

(1 + 2*6:100 ) * 500 = 1,12 * 500 = 560 (руб.)

Ответ: через полгода на вкладе будет 560 руб.

Сложный процентный рост.

В Сберегательном банке России для некоторых видов вкладов принята следующая система начисления денег. За первый год нахождения внесенной суммы на счете начисляется 40% от нее. В конце года вкладчик может снять со счета эти деньги – «проценты», как их обычно называют.

Если же он этого не сделал, то они присоединяются к начальному вкладу, и поэтому в конце следующего года 40% начисляются банком уже на новую, увеличенную сумму. Иначе говоря, при такой системе начисляются банком уже на новую, увеличенную сумму. Иначе говоря, при такой системе начисляются «проценты на проценты», или, как их обычно называют, сложные проценты.

Подсчитаем, сколько денег получит вкладчик через 3 года, если он положил на срочный счет в банк1000 руб. и ни разу не будет брать деньги со счета:

40% от 1000 руб. составляют 0,4 * 1000 = 400 руб., и следовательно, через год на его счете будет

1000 + 400 = 1400 (руб.)

40% от новой суммы 1400 руб. составляют 0,4 * 1400 = 560 руб., и следовательно, через 2 года на его счете будет

1400 + 560 = 1960 (руб.)

40% от новой суммы 1960 руб. составляют 0,4 * 1960 = 784 руб., и следовательно, через 3 года на его счете будет

1960 + 784 = 2744 (руб.)

Нетрудно представить себе, сколько при таком непосредственном , «лобовом» подсчёте понадобилось бы времени для нахождения суммы вклада через 10 лет. Между тем, подсчёт можно вести значительно проще.

Именно через год начальная сумма увеличится на 40%, то есть составит 140% от начальной, или, другими словами, увеличится в 1,4 раза. В следующем году новая, уже увеличенная сумма тоже увеличится на те же 40%. Следовательно, через 2 года начальная сумма увеличится в 1,4 * 1,4 = 1,4 2 раза.

Еще через один год и эта сумма увеличится в 1,4 раза, так что начальная сумма увеличится в 1,4 * 1,4 2 = 1,4 3 раза. При таком способе рассуждения получаем решение нашей задачи значительно более простое:

1,4 3 * 1000 = 2,744 * 1000 = 2744 (руб.)

Решим теперь эту задачу в общем виде. Пусть банк начисляет p % годовых, внесённая сумма равна S рублей, а сумма, которая будет на счёте через n лет, равна S_n рублей.

p % от S составляют p:100* S рублей, и через год на счёте окажется сумма

то есть начальная сумма увеличится в 1 + p:100 раза.

За следующий год сумма S ₁ увеличится во столько же раз, и поэтому через два года на счёте будет сумма

Аналогично, S ₃ =(1 + p:100 ) 3 S и так далее. Другими словами, справедливо равенство

Эту формулу называют формулой сложного процентного роста, или просто формулой сложных процентов.

Задача 1. Какая сумма будет на срочном счёте вкладчика через 4 года, если банк начисляет 10% годовых и внесённая сумма равна 2 000 рублей?

Подставим в формулу значения процентной ставки p = 10, количество лет n = 4 и величину первоначального вклада S = 2000, получим:

(1 + 10:100 ) 4 * 2000 = 1,1 4 * 2000 = 1,4641 * 2000 = 2928,2 (рублей).

Ответ: через 4 года на счёте будет сумма 2928,2 рубля.

Предположим, что вы хотите положить в банк 10 000 рублей, чтобы на них «росли проценты». В Сбербанке вам предложат 120% годовых, если вы кладёте деньги на 3 месяца, 130% годовых, если положите на 6 месяцев, и 150% годовых при вкладе на год.

В банке «Триумф» вам предложат 200% годовых при вкладе на год. Подсчитаем, сколько вы получите через 5 лет. Поскольку каждый год вы будете получать 200% годовых, то за 5 лет вы получите в 5 раз больше – 1000%, т.е. 100 000 рублей к своим 10 тысячам рублей. Но это не так!

Считать следует иначе! За год ваш вклад утраивается, т.е. через год у вас будет 30 тысяч рублей, а за второй год он еще утроится и составит 90 000 рублей. То же самое буде происходить после третьего, четвёртого и пятого года. Поэтому после третьего года у вас будет уже 270 000 рублей, после четвёртого 810 000 рублей, а после пятого – 2 430 000 рублей, а не 110 000 рублей, как мы предполагали сначала. Теперь стоит выбрать способ вложения денег: на 3 месяца, на 5 месяцев или на год.

Казалось бы, лучше всего положить на год, что даёт самый высокий процент годовых – 150%. Но, наученные расчётами с другими банками, давайте проверим.

Если положить на полгода из расчёта 130% годовых, то через полгода получим доход в 65% от вложенной суммы, т.е. сумма увеличится в 1,65 раз. Если затем еще раз положить на полгода все полученные деньги, то сумма возрастёт в 1,65 * 1,65 = 2,7225 раза, то есть на 172,25%, что существенно больше 150-ти процентов при вкладе сразу на год.

А если положить деньги на три месяца, потом еще на три, и еще, и еще раз на три месяца? В первый раз прибыль составит четверть от 120%, т.е. 30% от вложенной суммы. Это значит, что вклад увеличится в 1,3 раза. В следующий месяц он увеличится еще в 1,3 раза, что даст увеличение первоначальной суммы в 1,69 раза. Через следующие три месяца увеличение составит 2,197 раза, а к концу года получим увеличение в 2,8561 раза. Таким образом, получаем 185,61% годовых. Правда, при этом нужно приходить в банк каждые три месяца, чтобы забирать вклад и снова класть его на три месяца.

Но есть ещё форма вклада под 100% годовых с правом снять вклад в любое время с получением соответствующей доли прибыли. Вот, наверное, золотая жила! Ведь мы убедились, что чем чаще кладёшь и берёшь вклад, тем больше оказывается прибыль.

Если ходить в Сбербанк каждый день, то каждый раз вклад будет увеличиваться в 1+ 1:365 , а за год увеличение составит (1 + 1:365 ) 365 раза.

Величина числа (1 +1:n) n действительно увеличивается с увеличением n , но не может превзойти числа е = 2,71828… и стремится к этому числу с увеличением n .

Число е названо так в честь Леонардо Эйлера. Оно играет важную роль во многих разделах математики.

Итак, даже бегая в Сбербанк каждый час, нам не удастся получить доход больше 172% годовых, если мы примем эту форму вложения денег.

Ипотека — это заем, который предоставляет нам бан­ковское учреждение для того, чтобы мы могли опла­тить стоимость жилья. Когда банк одалживает нам деньги, мы должны вернуть ему эту сумму плюс соот­ветствующие проценты. Возвращение ипотечного кре­ дита осуществляется не в конце договорного срока, а ежегодными частями. Например, Эдуард купил себе квартиру, но так как у него не было для этого достаточно денег, он обратился в банк за ипотечным кредитом в один миллион рублей со сро­ ком погашения 20 лет. Тип годового процента является фиксированным: 4%. Какую сумму должен возвращать Эдуард банку ежегодно? Возвращаемая сумма называ­ется годовым погашением и рассчитывается следую­щим образом:

Как решать задачи с процентами?

Процентом называют вид десятичной дроби. Суть процента можно понять из названия, которое произошло от слова «cento», что в переводе означает «сто». Отсюда следует, что процент – это сотая доля от целого числа, принимаемая за единицу. Для обозначения процентов в математике и других областях науки используется знак %.

Нужно ли это обычному человеку?

Конечно, чаще всего, иметь дело с процентами приходится людям, деятельность которых связана с наукой. Не редко это счастье достается ученикам в рамках школьной программы математики. Однако, сфера применения процентов настолько широка, что с необходимостью их вычисления сталкиваются представители самых разных профессий и занятий. Аудитория нашего сайта – не исключение. Ведь перед дачниками часто стоит задача определения концентрации раствора удобрений, расчета налога на землю или другое имущество, определения размеров выплаты по кредиту и т.д.

Во всех этих случаях без умения правильно обращаться с процентами не обойтись. А они товарищи капризные, ошибок не любят. Поэтому, несмотря на кажущуюся простоту задач с процентами, при их решении необходимо соблюдать ряд определенных правил.

Все задачи, в которых фигурируют проценты, довольно просто решаются при использовании принципа пропорции. В чем заключается его суть? Например, нужно определить, чему равняется 76 % от числа 840? Для этого составляется соответствующая пропорция. В ней 840 приравнивается к 100 %. Искомая величина х – 76 %. Это позволяет составить следующее соотношение:

840 / х = 100 % / 76 % или 840 * 76 % = х * 100 %

Отсюда получается, что:
х = 840*76 % / 100 % = 638,4

Как видите, все предельно просто.

Основные типы задач с процентами

С точки зрения математики можно выделить 3 категории задач, решение которых связано с вычислением процентов.

Это когда необходимо найти процент от конкретного числа, заданного в условиях. Адаптируя пример к обстоятельствам жизни дачников можно привести следующую задачу. Предположим, что по законам какого-либо региона владелец частного земельного участка должен ежегодно выплачивать налог на землю. Размер его определяется как 2 % от кадастровой стоимости земли. Цена участка при этом 327 тыс. руб. Каков размер ежегодного налога? Чтобы ответить на поставленный вопрос, составляется пропорция:

327 тыс. руб. = 100 %;
Х тыс. руб. = 2 %.

Приводя эту зависимость к уравнению, получаем: х * 100 = 327 * 2. В результате: х = 327*2/100 = 6,54 тыс. руб.

Другой пример подобного рода задач связан с вопросом, который волнует подавляющее большинство дачников – прибавки к пенсиям или заработной плате. Предположим, сейчас пенсия человека составляет 7 200 руб., но со следующего месяца ее обещают увеличить на 15 %. Сколько это будет непосредственно в рублях? Опять составляется пропорция:

7 200 руб. = 100 %
х = 15 %

Далее: х*100 = 7 200*15; и соответственно х = 7 200*15/100 = 1 080. Таким образом, прибавка к пенсии составит 1 080 руб., после чего общая сумма составит 8 280 руб.

В данном случае предстоит решить обратную задачу, то есть по имеющемуся проценту вычислить число. Например, известно, что 10 кг некоего вещества входят в состав удобрения, при этом представляя собой 40 % от общего его количества. Нужно определить общую массу готового удобрения. Для этого также составляется пропорция, но вид она будет иметь немного другой:

10 кг – 40 %
х кг – 100%

Отсюда следует, что х = 10 * 100 / 40 = 25 кг.

К этой категории относятся задачи, в которых нужно через одно число определить процентное соотношение другого. К примеру, объем утреннего полива моркови должен составлять – 60 л. Вечером же на грядки нужно вылить 150 л. Сколько процентов от вечернего полива составляет утренний? Основное соотношение выглядит следующим образом:

150 л – 100 %;
60 л чашка – х %

Тогда: х = 60*100/ 150 = 40 %

Для тех дачников, которые рассматривают свой приусадебный участок, как источник дохода, должна быть интересной технология расчета рентабельности. Этот показатель используется в экономике как мера успешности предприятия и также рассчитывается в процентах. Именно по уровню рентабельности судят о том, насколько рационально организован производственный процесс.

Итак, основу расчета составляют две величины:

* полная себестоимость, включающая все денежные расходы, в том числе транспортные, а также покупку инвентаря и т.д.;

* доход, полученный от реализации собранного урожая.

Их разность представляет собой чистую прибыль. Пр = Д – С. При этом формула рентабельности имеет вид: Р = Пр/С*100 %. Таким образом, если общая себестоимость продукции составляет 8 200 руб., а продана она была за 9 000 руб., рентабельность будет равна: Р = (9 000 – 8 200)/8 200 *100 % = 9,75 %. Обычно, приемлемым уровнем рентабельности в экономике предприятия считается 5 %. При меньших показателях руководству рекомендуют искать варианты более рациональной организации труда.

В любом случае знать как решать задачи по алгебре с процентами нужно ещё в школе, а тогда дальше это не составит для вас труда.

Задачи на проценты

Рассмотрим три основных типа задач на проценты.

Нахождение процента от числа

Чтобы найти процент от числа, нужно число умножить на процент.

Задача № 1569 из учебника “Виленкин 5 класс”

Предприятие изготовило за квартал 500 насосов, из которых 60% имели высшую категорию качества. Сколько насосов высшей категории качества изготовило предприятие?

Найдем 60% от 500 (общее количество насосов).

500 · 0,6 = 300 насосов высшей категории качества.

Ответ: 300 насосов высшей категории качества.

Нахождение числа по его проценту

Чтобы найти число по его проценту, нужно его известную часть разделить на то, сколько процентов она составляет от числа.

Так как задачи «процент по числу» и «число по его проценту» очень похожи и часто не сразу понятно какой тип задачи перед нами, старайтесь внимательно читать текст. Если вам встречаются слова «который», «что составляет» и «который составляет», скорее всего перед вами задача «число по его проценту».

Задача № 1536 из учебника «Виленкин 5 класс»

Ученик прочитал 138 страниц, что составляет 23% числа всех страниц в книге. Сколько страниц в книге?

Итак, нам неизвестно сколько всего страниц в книге. Но мы знаем, что часть, которую прочитал ученик ( 138 страниц) составляет 23% от общего количества страниц в книге.

Так как 138 стр. — это всего лишь часть, само количество страниц, естественно, будет больше 138 . Это поможет нам при проверке.

Проверка: 600 > 138 (это означает, что 138 является частью 600 ).

Ответ: 600 (стр.) — общее количество страниц в книге.

Сколько процентов одно число составляет от другого

Чтобы найти, сколько процентов одно число составляет от другого, нужно ту часть, о которой спрашивается, разделить на общее количество и умножить на 100% .

Задача № 1609 из учебника «Виленкин 5 класс»

Из 200 арбузов 16 оказались незрелыми. Сколько процентов всех арбузов составили незрелый арбузы?

О чем спрашивают? О незрелых арбузах. Значит, 16 делим на общее количество арбузов и умножаем на 100% .

Ответ: 8% — составляют незрелые арбузы от всех арбузов.

Источники:

https://www.sites.google.com/site/jleibobl368/podgotovka-k-ege/zadaci-na-pocenty
https://www.kak-sdelat.su/2496-kak-reshat-zadachi-s-procentami.html
https://math-prosto.ru/?page=pages/percent/percent3.php