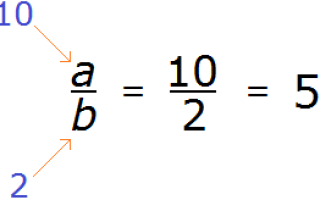Что такое множества чисел

Что такое множество?

Множество — это набор каких-либо объектов. Объекты, из которых состоит множество, называются элементами этого множества.

Например: множество школьников, множество машин, множество чисел .

В математике множество рассматривается намного шире. Мы не будем сильно углубляться в эту тему, поскольку она относится к высшей математике и на первых порах может создавать трудности для обучения. Мы рассмотрим только ту часть темы, с которой уже имели дело.

Обозначения

Множество чаще всего обозначают заглавными буквами латинского алфавита, а его элементы — строчными. При этом элементы заключаются в фигурные скобки.

Например, если наших друзей зовут Том, Джон и Лео , то мы можем задать множество друзей, элементами которого будут Том, Джон и Лео.

Обозначим множество наших друзей через заглавную латинскую букву F ( friends ), затем поставим знак равенства и в фигурных скобках перечислим наших друзей:

Пример 2 . Запишем множество делителей числа 6.

Обозначим через любую заглавную латинскую букву данное множество, например, через букву D

затем поставим знак равенства и в фигурных скобках перечислим элементы данного множества, то есть перечислим делители числа 6

Если какой-то элемент принадлежит заданному множеству, то эта принадлежность указывается с помощью знака принадлежности ∈ . К примеру, делитель 2 принадлежит множеству делителей числа 6 (множеству D ). Записывается это так:

Читается как «2 принадлежит множеству делителей числа 6«

Если какой-то элемент не принадлежит заданному множеству, то эта не принадлежность указывается с помощью зачёркнутого знака принадлежности ∉ . К примеру, делитель 5 не принадлежит множеству D . Записывается это так:

Читается как «5 не принадлежит множеству делителей числа 6«

Кроме того, множество можно записывать прямым перечислением элементов, без заглавных букв. Это может быть удобным, если множество состоит из небольшого количества элементов. Например, зададим множество из одного элемента. Пусть этим элементом будет наш друг Том:

Зададим множество, которое состоит из одного числа 2

Зададим множество, которое состоит из двух чисел: 2 и 5

Множество натуральных чисел

Это первое множество с которым мы начали работать. Натуральными числами называют числа 1, 2, 3 и т.д.

Натуральные числа появились из-за потребности людей сосчитать те иные объекты. Например, посчитать количество кур, коров, лошадей. Натуральные числа возникают естественным образом при счёте.

В прошлых уроках, когда мы употребляли слово «число» , чаще всего подразумевалось именно натуральное число.

В математике множество натуральных чисел обозначается заглавной латинской буквой N.

Например, укажем, что число 1 принадлежит множеству натуральных чисел. Для этого записываем число 1, затем с помощью знака принадлежности ∈ указываем, что единица принадлежит множеству N

Читается как: «единица принадлежит множеству натуральных чисел»

Множество целых чисел

Множество целых чисел включает в себя все положительные и отрицательные числа, а также число 0.

Множество целых чисел обозначается заглавной латинской буквой Z .

Укажем, к примеру, что число −5 принадлежит множеству целых чисел:

Укажем, что 10 принадлежит множеству целых чисел:

Укажем, что 0 принадлежит множеству целых чисел:

В будущем все положительные и отрицательные числа мы будем называть одним словосочетанием — целые числа.

Множество рациональных чисел

Рациональные числа, это те самые обыкновенные дроби, которые мы изучаем по сей день.

Рациональное число — это число, которое может быть представлено в виде дроби , где a — числитель дроби, b — знаменатель.

В роли числителя и знаменателя могут быть любые числа, в том числе и целые (за исключением нуля, поскольку на нуль делить нельзя).

Например, представим, что вместо a стоит число 10, а вместо b — число 2

10 разделить на 2 равно 5. Видим, что число 5 может быть представлено в виде дроби , а значит число 5 входит во множество рациональных чисел.

Легко заметить, что число 5 также относится и ко множеству целых чисел. Стало быть множество целых чисел входит во множество рациональных чисел. А значит, во множество рациональных чисел входят не только обыкновенные дроби, но и целые числа вида −2, −1, 0, 1, 2.

Теперь представим, что вместо a стоит число 12, а вместо b — число 5.

12 разделить на 5 равно 2,4. Видим, что десятичная дробь 2,4 может быть представлена в виде дроби , а значит она входит во множество рациональных чисел. Отсюда делаем вывод, что во множество рациональных чисел входят не только обыкновенные дроби и целые числа, но и десятичные дроби.

Мы вычислили дробь и получили ответ 2,4. Но мы могли бы выделить в этой дроби целую часть:

При выделении целой части в дроби , получается смешанное число . Видим, что смешанное число тоже может быть представлено в виде дроби . Значит во множество рациональных чисел входят и смешанные числа.

В итоге мы приходим к выводу, что множество рациональных чисел содержат в себе:

• целые числа
• обыкновенные дроби
• десятичные дроби
• смешанные числа

Множество рациональных чисел обозначается заглавной латинской буквой Q.

Например укажем, что дробь принадлежит множеству рациональных чисел. Для этого записываем саму дробь , затем с помощью знака принадлежности ∈ указываем, что дробь принадлежит множеству рациональных чисел:

∈ Q

Укажем, что десятичная дробь 4,5 принадлежит множеству рациональных чисел:

Укажем, что смешанное число принадлежит множеству рациональных чисел:

∈ Q

Вводный урок по множествам завершён. В будущем мы рассмотрим множества намного лучше, а пока рассмотренного в данном уроке будет достаточно.

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Обозначение, запись и изображение числовых множеств

Из большого количества разнообразных множеств особо интересными и важными являются числовые множества, т.е. те множества, элементами которых служат числа. Очевидно, что для работы с числовыми множествами необходимо иметь навык записи их, а также изображения их на координатной прямой.

Запись числовых множеств

Общепринятым обозначением любых множеств являются заглавные буквы латиницы. Числовые множества – не исключение. К примеру, мы можем говорить о числовых множествах B , F или S и т.п. Однако есть также общепринятая маркировка числовых множеств в зависимости от входящих в него элементов:

N – множество всех натуральных чисел; Z – множество целых чисел; Q – множество рациональных чисел; J – множество иррациональных чисел; R – множество действительных чисел; C – множество комплексных чисел.

Становится понятным, что обозначение, например, множества, состоящего из двух чисел: – 3 , 8 буквой J может ввести в заблуждение, поскольку этой буквой маркируется множество иррациональных чисел. Поэтому для обозначения множества – 3 , 8 более подходящим будет использование какой-то нейтральной буквы: A или B , например.

Напомним также следующие обозначения:

• ∅ – пустое множество или множество, не имеющее составных элементов;
• ∈ или ∉ – знак принадлежности или непринадлежности элемента множеству. Например, запись 5 ∈ N обозначает, что число 5 является частью множества всех натуральных чисел. Запись – 7 , 1 ∈ Z отражает тот факт, что число – 7 , 1 не является элементом множества Z , т.к. Z – множество целых чисел;
• знаки принадлежности множества множеству:
  ⊂ или ⊃ – знаки «включено» или «включает» соответственно. Например, запись A ⊂ Z означает, что все элементы множества А входят в множество Z , т.е. числовое множество A включено в множество Z . Или наоборот, запись Z ⊃ A пояснит, что множество всех целых чисел Z включает множество A .
  ⊆ или ⊇ – знаки так называемого нестрогого включения. Означают «включено или совпадает» и «включает или совпадает» соответственно.

Рассмотрим теперь схему описания числовых множеств на примере основных стандартных случаев, наиболее часто используемых на практике.

Первыми рассмотрим числовые множества, содержащие конечное и небольшое количество элементов. Описание подобного множества удобно составлять, просто перечисляя все его элементы. Элементы в виде чисел записываются, разделяясь запятой, и заключаются в фигурные скобки (что соответствует общим правилам описания множеств). К примеру, множество из чисел 8 , – 17 , 0 , 15 запишем как < 8 , - 17 , 0 , 15 >.

Случается, что количество элементов множества достаточно велико, но все они подчиняются определенной закономерности: тогда в описании множества используют многоточие. К примеру, множество всех четных чисел от 2 до 88 запишем как: < 2 , 4 , 6 , 8 , … , 88 >.

Теперь поговорим об описании числовых множеств, в которых количество элементов бесконечно. Иногда их описывают при помощи того же многоточия. Например, множество всех натуральных чисел запишем так: N = < 1 , 2 , 3 , … >.

Также возможно записать числовое множество с бесконечным количеством элементов при помощи указания свойств его элементов. Применяют при этом обозначение < х | свойства >. К примеру, < n | 8 · n + 3 , n ∈ N >определяет множество натуральных чисел, которые при делении на 8 дадут остаток 3 . Это же множество возможно записать как: < 11 , 19 , 27 , … >.

В частных случаях числовые множества с бесконечным количеством элементов – это общеизвестные множества N , Z , R и т.д., либо числовые промежутки. Но в основном числовые множества представляют собой объединение составляющих их числовых промежутков и числовых множеств с конечным количеством элементов (о них мы говорили в самом начале статьи).

Рассмотрим на примере. Допустим, составляющими некого числового множества являются числа – 15 , – 8 , – 7 , 34 , 0 , а также все числа отрезка [ – 6 , – 1 , 2 ] и числа открытого числового луча ( 6 , + ∞ ) . В соответствии с определением объединения множеств заданное числовое множество запишем как: < - 15 , - 8 , - 7 , 34 >∪ [ – 6 , – 1 , 2 ] ∪ < 0 >∪ ( 6 , + ∞ ) . Подобная запись фактически означает множество, включающее в себя все элементы множеств < - 15 , - 8 , - 7 , 34 , 0 >, [ – 6 , – 1 , 2 ] и ( 6 , + ∞ ) .

Таким же образом, объединяя различные числовые промежутки и множества отдельных чисел, возможно дать описание любому числовому множеству, состоящему из действительных чисел. На основе сказанного становится понятно, для чего вводятся различные виды числовых промежутков, такие как интервал, полуинтервал, отрезок, открытый числовой луч и числовой луч. Все эти виды промежутков совместно с обозначениями множеств отдельных чисел дают возможность через их объединение описать любое числовое множество.

Необходимо также обратить внимание на то, что отдельные числа и числовые промежутки при записи множества могут быть упорядочены по возрастанию. В общем, это не является обязательным требованием, однако подобное упорядочивание позволяет представить числовое множество проще, а также верно отобразить его на координатной прямой. Также стоит уточнить, что в таких записях не применяют числовые промежутки с общими элементами, поскольку эти записи возможно заменить объединением числовых промежутков, исключив общие элементы. К примеру, объединением числовых множеств с общими элементами [ – 15 , 0 ] и ( – 6 , 4 ) будет полуинтервал [ – 15 , 4 ) . То же имеет отношение и к объединению числовых промежутков с одинаковыми граничными числами. Например, объединение ( 4 , 7 ] ∪ ( 7 , 9 ] является множеством ( 4 , 9 ] . Этот пункт подробно будет рассмотрен в теме нахождения пересечения и объединения числовых множеств.

Изображение числовых множеств на координатной прямой

В практических примерах удобно использовать геометрическое толкование числовых множеств – их изображение на координатной прямой. К примеру, такой способ поможет при решении неравенств, в которых нужно учесть ОДЗ – когда нужно отобразить числовые множества, чтобы определить их объединение и/или пересечение.

Мы знаем, что между точками координатной прямой и действительными числами имеется однозначное соответствие: вся координатная прямая есть геометрическая модель множества всех действительных чисел R . Следовательно, для изображения множества всех действительных чисел начертим координатную прямую и нанесем штриховку на всем ее протяжении:

Зачастую и не указывают начало отсчета и единичный отрезок:

Рассмотрим изображение числовых множеств, состоящих из конечного количества отдельных чисел. К примеру, отобразим числовое множество < - 2 , - 0 , 5 , 1 , 2 >. Геометрической моделью заданного множества станут три точки координатной прямой с соответствующими координатами:

В большинстве случаев возможно не соблюдать абсолютную точность чертежа: вполне достаточно схематичного изображения без соблюдения масштаба, но с сохранением взаимного расположения точек относительно друг друга, т.е. любая точка с бОльшей координатой должна быть правее точки с меньшей. С учётом сказанного уже имеющийся чертеж может выглядеть так:

Отдельно из возможных числовых множеств выделяют числовые промежутки интервалы, полуинтервалы, лучи и пр.)

Теперь рассмотрим принцип изображения числовых множеств, являющихся объединением нескольких числовых промежутков и множеств, состоящих их отдельных чисел. В этом нет никакой сложности: согласно определению объединения на координатной прямой необходимо отобразить все составляющие множества заданного числового множества. Например, создадим иллюстрацию числового множества ( – ∞ , – 15 ) ∪ < - 10 >∪ [ – 3 , 1 ) ∪ < log 2 5 , 5 >∪ ( 17 , + ∞ ) .

Также довольно распространены случаи, когда числовое множество, которое необходимо изобразить, включает в себя все множество действительных чисел кроме одной или нескольких точек. Подобные множества часто задаются условиями вроде х ≠ 5 или х ≠ – 1 и т.п. В таких случаях множества в своей геометрической модели являются всей координатной прямой за исключением заданных точек. Общепринято говорить, что эти точки необходимо «выколоть» из координатной прямой. Изображается выколотая точка кружочком с пустым центром. Чтобы подкрепить сказанное практическим примером, отобразим на координатной прямой множество с заданным условием х ≠ – 2 и х ≠ 3 :

Информация, приведенная в данной статье, призвана помочь получить навык видеть запись и изображение числовых множеств так же легко, как и отдельных числовых промежутков. В идеале записанное числовое множество сразу должно представляться в виде геометрического образа на координатной прямой. И наоборот: по изображению должно с легкостью формироваться соответствующее числовое множество через объединение числовых промежутков и множеств, являющихся отдельными числами.

Основные числовые множества

Число — абстракция, используемая для количественной характеристики объектов. Числа возникли еще в первобытном обществе в связи с потребностью людей считать предметы. С течением времени по мере развития науки число превратилось в важнейшее математическое понятие.

Для решения задач и доказательства различных теорем необходимо понимать, какие бывают виды чисел. Основные виды чисел включают в себя: натуральные числа, целые числа, рациональные числа, действительные числа.

Основные числовые множества

Натуральные числа – это числа, получаемые при естественном счёте предметов, а вернее при их нумерации («первый», «второй», «третий». ). Множество натуральных чисел обозначается латинской буквой N (можно запомнить, опираясь на английское слово natural). Можно сказать, что N =

Целые числа – это числа из множества <0, 1, -1, 2, -2, . >. Это множество состоит из трех частей – натуральные числа, отрицательные целые числа (противоположные натуральным числам) и число 0 (нуль). Целые числа обозначаются латинской буквой Z. Можно сказать, что Z =<. -2,-1,0,1,2. >.

Рациональные числа – это числа, представимые в виде дроби m/n, где m — целое число, а n — натуральное число. Для обозначения рациональных чисел используется латинская буква Q. Все натуральные и целые числа – рациональные. Также в качестве примеров рациональных чисел можно привести: 1/2, 2/7, -11/3.

Действительные (вещественные) числа – это числа, которое применяются для измерения непрерывных величин. Множество действительных чисел обозначается латинской буквой R. Действительные числа включают в себя рациональные числа и иррациональные числа. Иррациональные числа – это числа, которые получаются в результате выполнения различных операций с рациональными числами (например, извлечение корня, вычисление логарифмов), но при этом не являются рациональными.

Любое действительное число можно отобразить на числовой прямой:

Комплексные числа – числа, являющиеся расширением множества действительных чисел. Они могут быть записаны в виде z = x + iy, где i — т. н. мнимая единица, для которой выполняется равенство i 2 = -1. Комплексные числа используются при решении задач электротехники, гидродинамики, картографии, квантовой механики, теории колебаний, теории хаоса, теории упругости и многих других. Комплексные числа подразделяются на алгебраические и трансцендентные. При этом каждое действительное трансцендентное является иррациональным, а каждое рациональное число — действительным алгебраическим. Более общими (но всё ещё счётными) классами чисел, чем алгебраические, являются периоды, вычислимые и арифметические числа (где каждый последующий класс шире, чем предыдущий).

Для перечисленных множеств чисел справедливо следующее выражение:

Т. е. множество натуральных чисел входит во множество целых чисел. Множество целых чисел входит во множество рациональных чисел. Множество рациональных чисел входит во множество действительных чисел. А множество действительных чисел входит во множество комплексных чисел.

Это высказывание можно проиллюстрировать с помощью кругов Эйлера:

Источники:

https://spacemath.xyz/chto_takoe_mnojestvo/
https://zaochnik.com/spravochnik/matematika/sets/oboznachenie-zapis-i-izobrazhenie-chislovyh-mnozhe/
https://calculatorium.ru/article/2